元启发式算法概述

元启发式算法概述

首先要了解什么是元启发式算法，以及分清其与启发式算法的区别。

启发式算法（heuristic algorithm）

指通过对过去经验的归纳推理以及实验分析来解决问题的方法，即借助于某种直观判断或试探的方法，以求得问题的次优解或以一定的概率求其最优解，所以可以认为启发式算法一种基于经验或者实验算法的统称。

  • 通常基于自然界中发现的一些规律或者准则
  • 能够被计算机计算和处理
  • 目标是得出最优解的近似解，但不能确定得到的解就是最优解
    • 但通常得到的解比局部最优解要好
  • 适用于不同的问题，并能同时考虑一些约束条件

元启发式算法（metaheuristic algorithm）

元启发式算法都从自然界的一些现象取得灵感(e.g.模拟退火、遗传算法)通过这些现象获取的求解过程（元启发式算法）来解决实际的一些问题。

元启发式算法可以看成是构造启发式算法的一些基础方法，而启发式算法就是利用元启发式算法，结合被求解问题的特征，设计出来的面向特定问题的算法。

  • 经典的启发式算法（元启发式算法）
    • 模拟退火（Simulated annealing）
    • 禁忌搜素（Tabu search）
    • 遗传算法（Genetic algorithms）
    • 蚁群算法（Ant colonies）

启发式算法元启发式算法问题特征

概括来说，启发式算法只做两件事：局部搜索 和 跳出局部

局部搜索

局部搜索算法设计的思想如下：

  1. 对于当前解
  2. while 未满足停止条件时 do
  3.   选择 （当前解的临近解）
  4.   if then
  5. end while

即以当前解为基础，不断在其附近找一个更好的解作为答案。
但如此往复会陷入局部最优解，可能错失其他的更好的解（全局最优解）。
因此，如何优雅地跳出局部最优解也是一门值得研究的学问。
例如，设计算法时考虑给出一定的概率去接受一些不那么好的解。
因为将这些不那么好的解作为当前解再搜索时，或许目标区域就会到另一个山沟里。

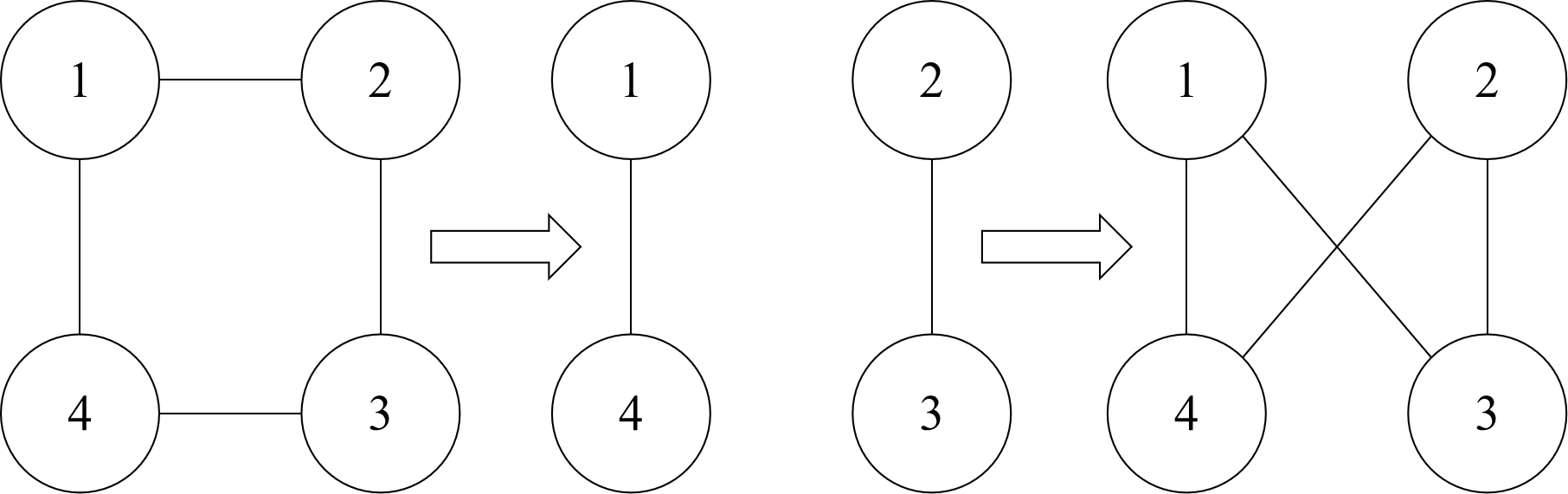
2-opt 算法

在旅行商问题中，去除某一回路 的两条边 e1 和 e2，形成了两个子图，对这两个子图重新连接形成新的回路 ， 是通过对 的 2-opt 变换形成的。

2-opt示意图

对于其中的某一回路 ，通过 2-opt 变换生成所有新的回路 对的变换，这些回路（包括 ）中的最优回路，为 2-opt 算法得出的解，即： 伪代码如下：

Algorithm 1 2-opt 算法

  1. Input: 完全图 的一个回路
  2. Output: 局部优化后的回路
  4. for do
  5.  for do
  6.   if 和 在 中有相邻的节点 then
  7.    continue // 要找不共点的两条边，否则重连等于原状态
  8.   end if
  9.  
  10.  if then
  11.    
  12.   end if
  13.  end for
  14. end for
  15. Return

2-opt 算法的时间复杂度为

3-opt 算法

3-opt 算法和 2-opt 算法相似，对回路 ，去除 3 条边，形成 3 个子路径，再通过 3 条边将这 3 个子路径连接起来，重新形成一个回路 。对 3 个子路径通过 3 条边连成一个回路，可以有 8 种不同的方式（包括原来的回路）。